Published on 31 May 2022.

Blog deneyiminizi iyileştirmek için öneri şarkı:
Bilgisayarların çalışmasının en büyük yardımcısı matrislerin programlanabilirliğini oluşturan en önemli Matematiksel Algoritmalardan biri olan LU Ayrışımının özelleşmiş bir algoritması : DooLittle Algoritması
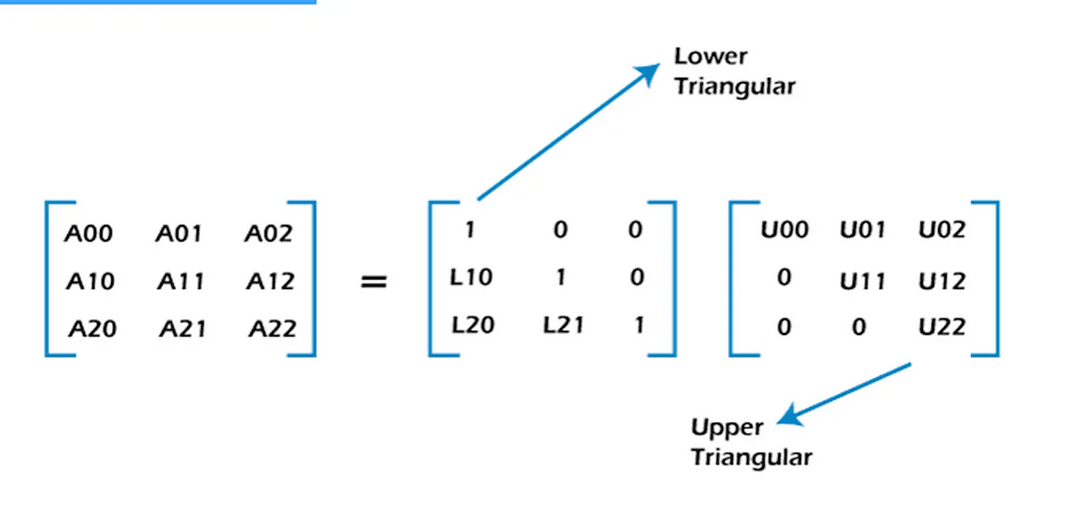
Bilgisayarlar kare matris sistemlerinin Lineer Denklemlerini çözerken çoğunlukla LU Ayrışımını kullanır.Bu yöntem matrisin tersini almada ve determinantını hesaplamada etkin bir yoldur.LU Ayrışımın özelleşmiş bir hali olan DooLittle Algoritmasını ele alalım.LU Ayrışımında, kare matrisimizi Lower Triangular ve Upper Triangular iki matrisin çarpımı olarak ele alırız.
●[A] = [L] [U]
Doolittle,LU Ayrışımının özelleşmiş bir hali olduğundan Doolittle Algoritmasında Lower Triangular Matrisimizin köşegen elemanları birim eleman skalerine eşittir.Doolittle ile beraber Gausss Eliminasyonunu yapmamıza gerek kalmaz.
DooLittle Algoritması basamakları:
●A, B, ve X matrislerini oluştur. A matrisim Augmented(Arttırılmış) Matris yapısında,B sabitler, X bilinmeyenler matrisidir.
●A = LU Ayrışımında U Upper Triangular matris, L Lower Triangular matrisimizdir. L matrisimizin köşegen elemanları 1' e eşittir.
●Ly = B. Denklemi y için çözeriz.
●Ux = y. X vektörünün değişkenleri için denklem çözülür

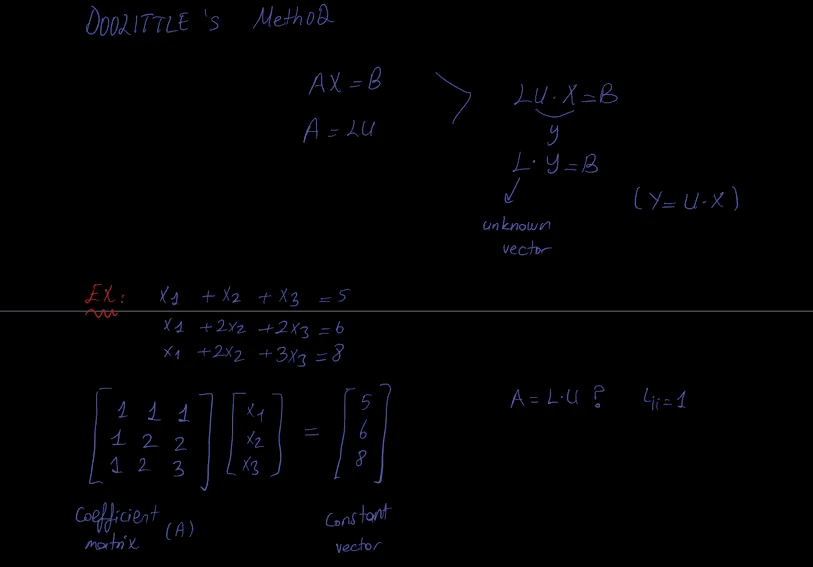
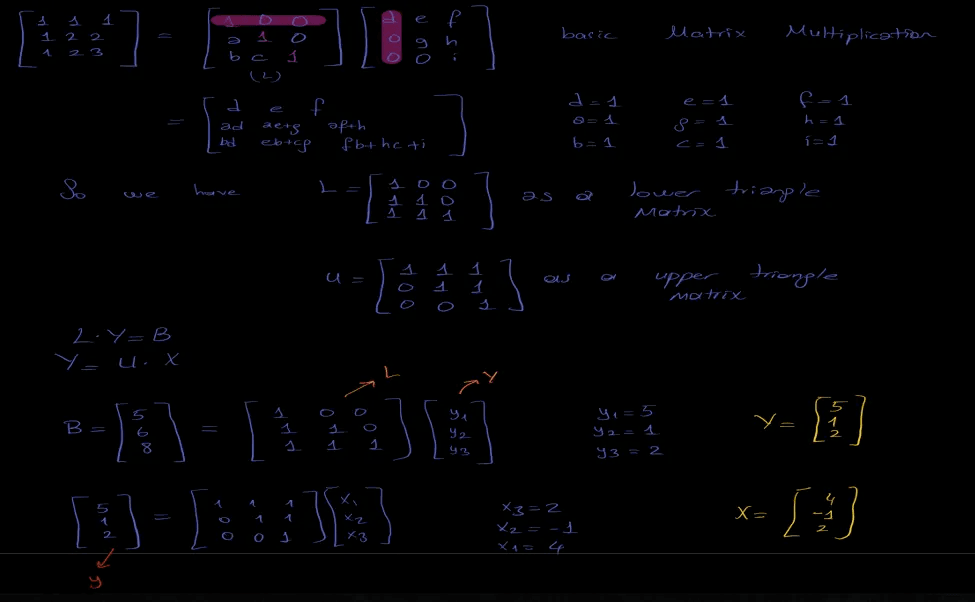
Hadi Uygulamaya dökelim.
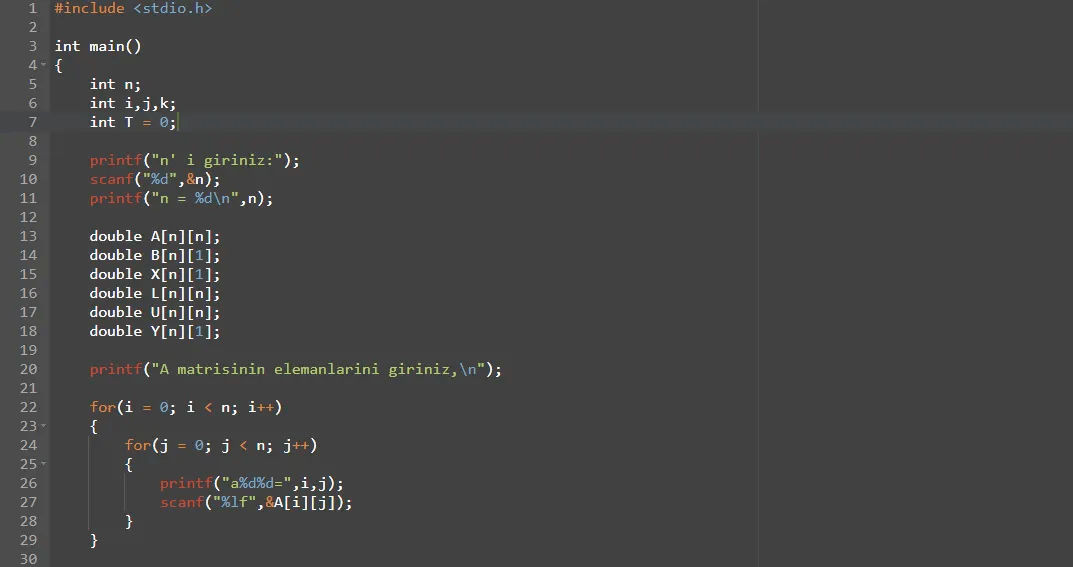
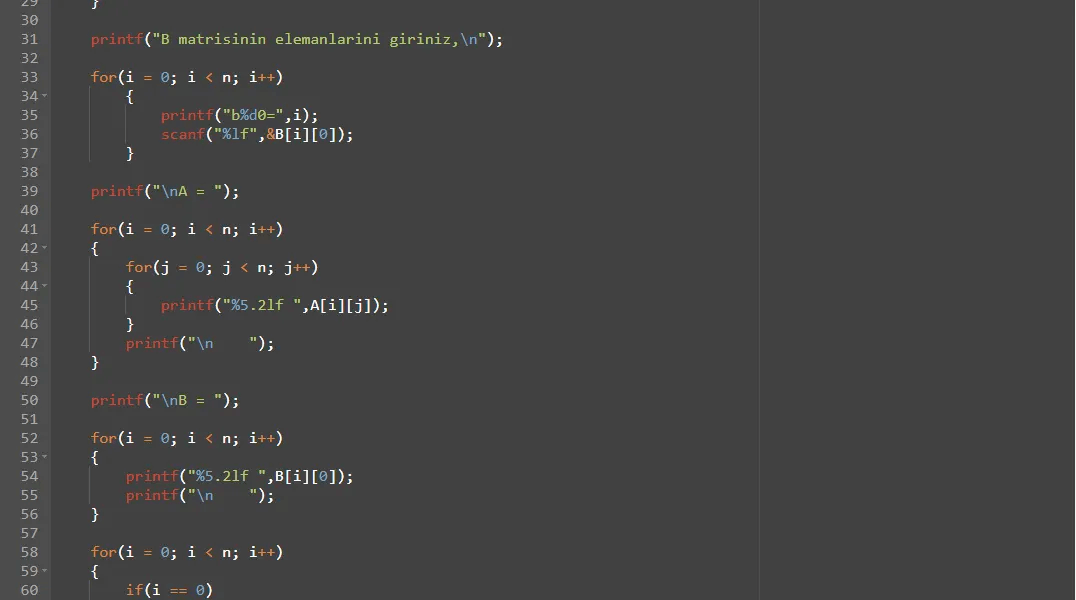
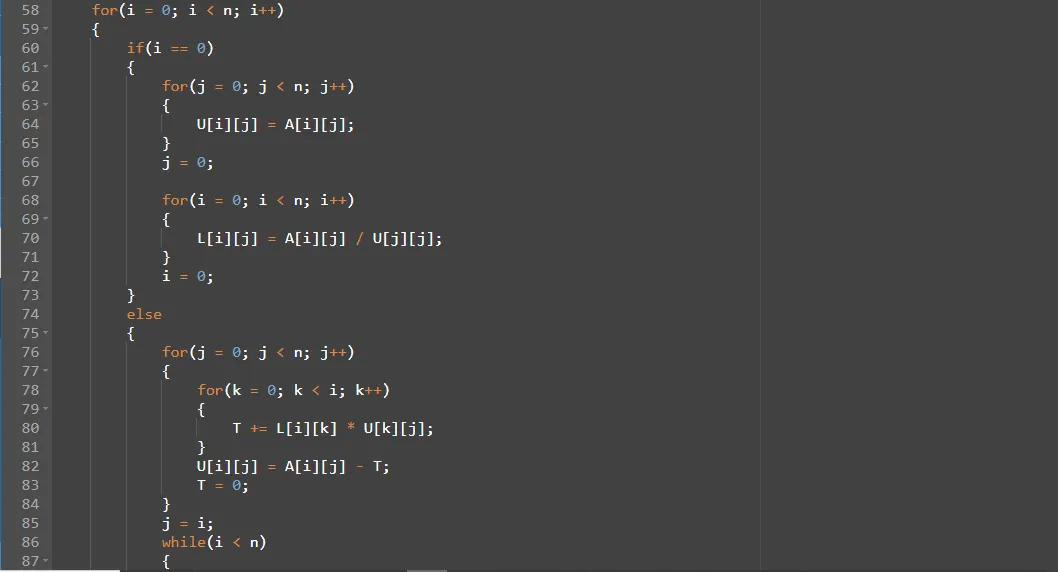
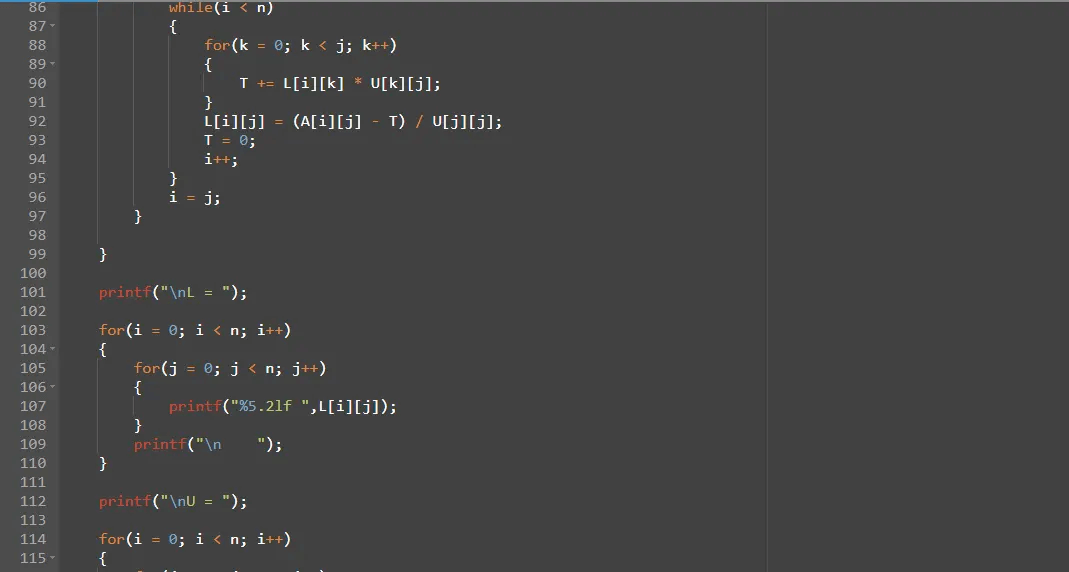
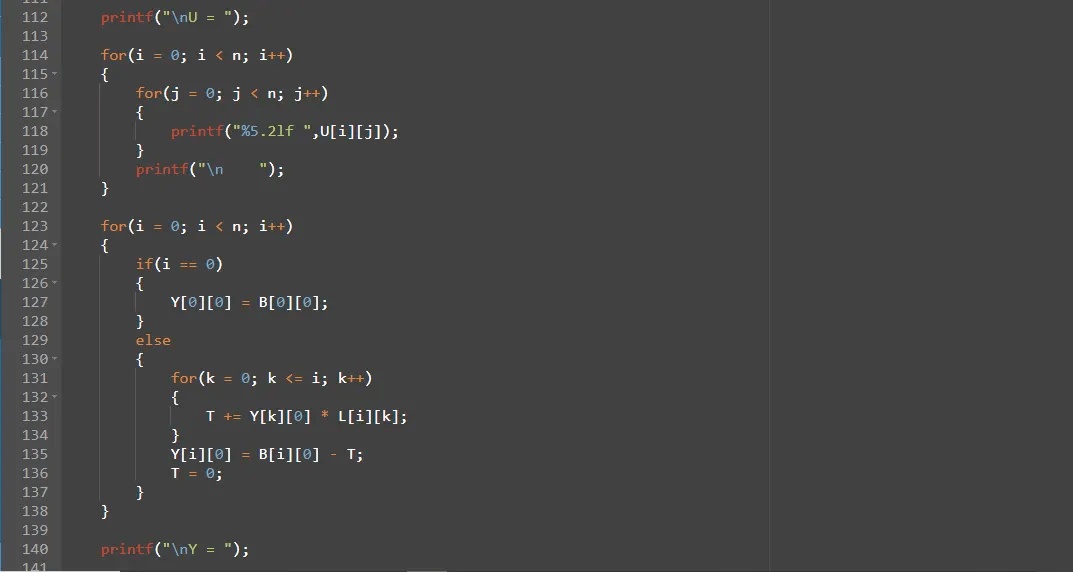
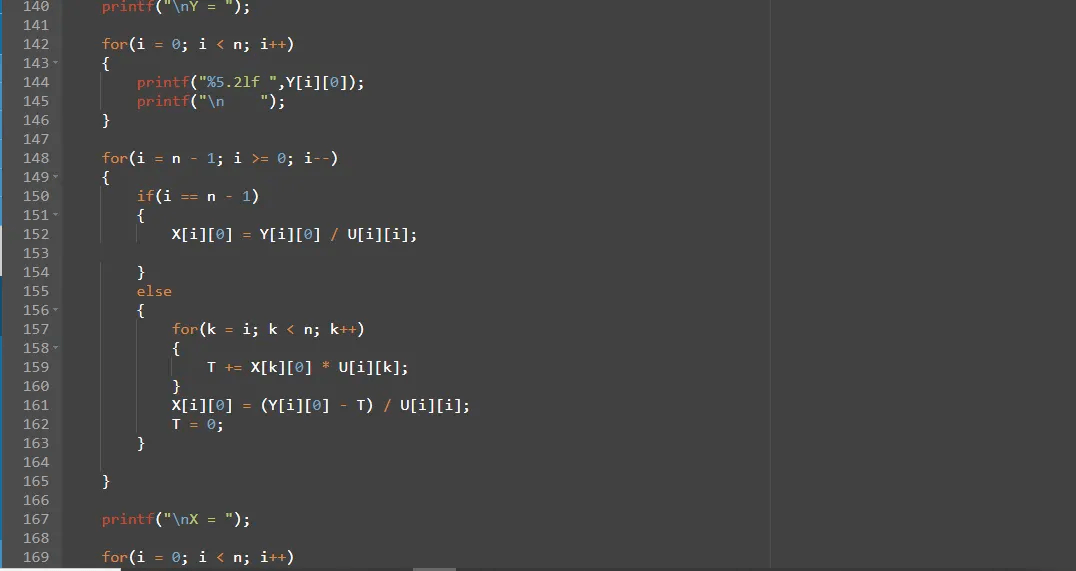
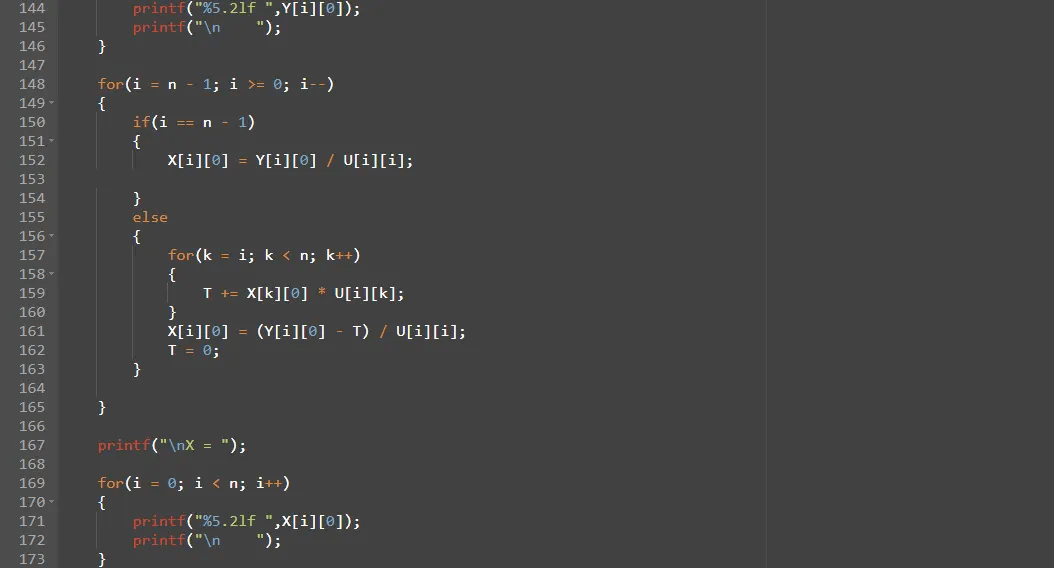
Bu içerik Yıldız Teknik Üniversitesi Bilgisayar Programlama 2 dersi için takım arkadaşım ile beraber üretilmiştir.